728x90
반응형
문제 설명
N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.
예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.
제한 사항
- sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
- sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
- 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.
입출력 예
| sticker | answer |
| [14, 6, 5, 11, 3, 9, 2, 10] | 36 |
| [1, 3, 2, 5, 4] | 8 |
입출력 예 설명
입출력 예 #1
6, 11, 9, 10이 적힌 스티커를 떼어 냈을 때 36으로 최대가 됩니다.
입출력 예 #2
3, 5가 적힌 스티커를 떼어 냈을 때 8로 최대가 됩니다.
풀이
- 수많은 삽질이 있었으나 정리하던 것이 사라졌고, 다시 정리함
- 우선
- sticker 길이가 3보다 작으면 3개 중에 한개라서 그냥 max로 리턴하면 됨
- OXX
- XOX
- XXO
- 짝수일 때는
- 배열 2개 만들어서 더 큰 쪽을 리턴
- OXOXOXOX
- XOXOXOXO
- 홀수일 때는
- 이때 머리가 뽀개지는데, 아래처럼 되어 있다.
- OXOXOXOXX
- XOXOXOXOX
- XXOXOXOXO
- OXXOXOXOX
- XOXXOXOXO
- OXOXXOXOX
- XOXOXXOXO
- 근데 또 잘 보니... XX만 옮겨다니는 것이잖아?
- 그럼 그걸 어떻게 만드냐... ㅋㅋㅋ
- 옮겨다닐 때 홀짝이 바뀌는데?
- 앞부분이랑 뒷부분도 다르네...
- 어떻게 안되냐 ㅋㅋㅋ
- X]OXOXOXO[X
- [XX]OXOXOXO -> a
- O[XX]OXOXOX a랑 b랑 [XX] 빼고 같잖아?
- XO[XX]OXOXO -> b
- OXO[XX]OXOX 그럼 [XX]가 제일 작은 애가 제일 큰 거 아닌가?
- XOXO[XX]OXO 아님. 앞이랑 뒤가 틀어져있어
- OXOXO[XX]OX
- XOXOXO[XX]O
- OXOXOXO[XX]
- X]OXOXOXO[X
- 어떻게 안되냐 2
- X]OXOXOXO[X -> 이건 그냥 홀수랑 같음
- [XX]OXOXOXO 앞 : 홀수 + XX + 뒤 : 짝수
- O[XX]OXOXOX 앞 : 짝수 + XX + 뒤 : 홀수
- XO[XX]OXOXO
- OXO[XX]OXOX
- 이때 머리가 뽀개지는데, 아래처럼 되어 있다.
- 아....................... 삽질이었다.
def solution(sticker):
answer = 0
n = len(sticker)
if n <= 3:
answer = max(sticker)
elif n % 2 == 0:
sum_even_sticker = sum([sticker[i] for i in range(0,n,2)])
sum_odd_sticker = sum([sticker[i] for i in range(1,n,2)])
answer = max(sum_even_sticker, sum_odd_sticker)
else:
front = [0 for _ in range(n)]
back = [0 for _ in range(n)]
front[0] = sticker[0]
front[1] = sticker[1]
back[n-2] = sticker[n-2]
back[n-1] = sticker[n-1]
for i in range(2,n-1,1):
front[i] = sticker[i] + front[i-2]
for i in range(n-3,0,-1):
back[i] = sticker[i] + back[i+2]
answer = max(front[n-3], back[1], back[2])
for i in range(1, n-2, 1):
if answer < front[i-1] + back[i+2]:
answer = front[i-1] + back[i+2]
return answer- 계속 번갈아 가며 뜯는 걸 상정하고 간단하게 풀려고 머리도 안쓰고...
- 누가 좀 때려줘... ㅠ.ㅠ;
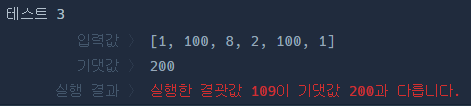
- 무조건 번갈아가며 뜯어내는게 아닌데... ㅡ.ㅡ;
- OXO와 OXXO의 조합으로 찾아야 한다.
- 구간 합이 제일 큰걸 합쳐야 하나?
- 첫번째 숫자 -> 다음숫자는X -> 그다음과 그 다음다음 중에 큰 숫자
- 1 -> 8 -> 100 = 109
- 두번쨰 숫자 -> 다음숫자는X -> 그다음과 그 다음다음 중에 큰 숫자
- 100 -> 100 = 200
- DP로 삽질하다 겨우 풀었다.
- 처음 시도했던 건
- dp[i] = sticker[i] + max(dp[i-2], dp[i-3])
- 뭔가 잘 안되고 print()를 해보면, 맨 앞숫자를 겟하고 맨 마지막 숫자도 겟해서 초과
- 두번째로 시도했던 건, 너무 많이 고쳐서 기억에 없다.
- 대충 OXXO랑 OXO중에 골라야 되는거,
- 맨 앞에 숫자랑 맨 뒤에 숫자랑 함께 고르지 않도록 하는거
- 그래서 for문 두번 돌리는 걸로 해결함.
def solution(sticker):
answer = 0
n = len(sticker)
if n <= 3:
answer = max(sticker)
else:
dp = [0] * n
for i in range(1,n):
dp[i] = max(sticker[i] + dp[i-2], dp[i-1])
answer = dp[-1]
dp[0] = sticker[0]
dp[1] = sticker[0]
for i in range(2,n-1):
dp[i] = max(sticker[i] + dp[i-2], dp[i-1])
answer = max(answer, dp[-2])
return answer- 점점 어쩌다 보니 풀리는 케이스가 많아진다.ㅋㅋㅋ
- 무지성 코딩 하지말고 이젠 설계를 하자구... ㅠ.ㅠ
- 하지만 무지성 코딩이 재밌어
정확성 테스트
테스트 1 〉 통과 (0.00ms, 10.4MB)
테스트 2 〉 통과 (0.00ms, 10.2MB)
테스트 3 〉 통과 (0.01ms, 10.2MB)
테스트 4 〉 통과 (0.01ms, 10.3MB)
테스트 5 〉 통과 (0.01ms, 10.2MB)
테스트 6 〉 통과 (0.02ms, 10.1MB)
테스트 7 〉 통과 (0.51ms, 10.4MB)
테스트 8 〉 통과 (0.82ms, 10.2MB)
테스트 9 〉 통과 (1.03ms, 10.3MB)
테스트 10 〉 통과 (0.52ms, 10.1MB)
테스트 11 〉 통과 (0.53ms, 10.3MB)
테스트 12 〉 통과 (0.52ms, 10.3MB)
테스트 13 〉 통과 (0.52ms, 10.3MB)
테스트 14 〉 통과 (0.52ms, 10.1MB)
테스트 15 〉 통과 (0.52ms, 10.3MB)
테스트 16 〉 통과 (0.53ms, 10.3MB)
테스트 17 〉 통과 (0.51ms, 10.2MB)
테스트 18 〉 통과 (0.91ms, 10.1MB)
테스트 19 〉 통과 (0.53ms, 10.3MB)
테스트 20 〉 통과 (0.53ms, 10.2MB)
테스트 21 〉 통과 (0.52ms, 10.2MB)
테스트 22 〉 통과 (0.52ms, 10.2MB)
테스트 23 〉 통과 (0.53ms, 10.1MB)
테스트 24 〉 통과 (0.53ms, 10.3MB)
테스트 25 〉 통과 (0.51ms, 10.1MB)
테스트 26 〉 통과 (0.51ms, 10.2MB)
테스트 27 〉 통과 (0.74ms, 10.1MB)
테스트 28 〉 통과 (0.50ms, 10.2MB)
테스트 29 〉 통과 (1.04ms, 10.1MB)
테스트 30 〉 통과 (0.55ms, 10.3MB)
테스트 31 〉 통과 (0.52ms, 10.1MB)
테스트 32 〉 통과 (1.06ms, 10.2MB)
테스트 33 〉 통과 (0.00ms, 10.2MB)
효율성 테스트
테스트 1 〉 통과 (56.92ms, 13.7MB)
테스트 2 〉 통과 (56.68ms, 13.8MB)
테스트 3 〉 통과 (57.94ms, 13.8MB)
테스트 4 〉 통과 (56.33ms, 14.3MB)- 고수의 풀이
- for문 한번으로 안되나 싶었는데... 역시 안되는 것 같다.
def solution(stickers):
if len(stickers) < 4:
return max(stickers)
n = len(stickers)
dp = [[0] * n for _ in range(2)]
dp[0][0] = stickers[0] # 0 번째 row는 첫 번째 스티커를 뜯음
dp[0][1] = dp[0][0]
dp[0][2] = dp[0][0]
dp[1][0] = 0 # 1 번째 row는 첫 번째 스티커를 뜯지 않음
dp[1][1] = stickers[1]
dp[1][2] = max(stickers[2] + dp[1][0], dp[1][1])
for i in range(3, n):
dp[0][i] = max(stickers[i - 1] + dp[0][i - 2], dp[0][i-1])
dp[1][i] = max(stickers[i] + dp[1][i - 2], dp[1][i - 1])
return max(dp[0][n - 2], dp[0][n - 1], dp[1][n - 1])
정확성 테스트
테스트 1 〉 통과 (0.00ms, 10.3MB)
테스트 2 〉 통과 (0.00ms, 10.3MB)
테스트 3 〉 통과 (0.02ms, 10.3MB)
테스트 4 〉 통과 (0.01ms, 10.2MB)
테스트 5 〉 통과 (0.01ms, 10.2MB)
테스트 6 〉 통과 (0.02ms, 10.3MB)
테스트 7 〉 통과 (1.14ms, 10.2MB)
테스트 8 〉 통과 (0.61ms, 10.3MB)
테스트 9 〉 통과 (0.61ms, 10.3MB)
테스트 10 〉 통과 (0.68ms, 10.1MB)
테스트 11 〉 통과 (0.63ms, 10.2MB)
테스트 12 〉 통과 (0.61ms, 10.3MB)
테스트 13 〉 통과 (0.83ms, 10.2MB)
테스트 14 〉 통과 (0.65ms, 10.3MB)
테스트 15 〉 통과 (0.61ms, 10.1MB)
테스트 16 〉 통과 (0.60ms, 10.3MB)
테스트 17 〉 통과 (0.61ms, 10.3MB)
테스트 18 〉 통과 (0.61ms, 10.3MB)
테스트 19 〉 통과 (0.61ms, 10.2MB)
테스트 20 〉 통과 (0.66ms, 10.3MB)
테스트 21 〉 통과 (1.07ms, 10.2MB)
테스트 22 〉 통과 (0.82ms, 10.2MB)
테스트 23 〉 통과 (0.61ms, 10.2MB)
테스트 24 〉 통과 (0.61ms, 10.2MB)
테스트 25 〉 통과 (0.61ms, 10.2MB)
테스트 26 〉 통과 (0.61ms, 10.1MB)
테스트 27 〉 통과 (0.64ms, 10.3MB)
테스트 28 〉 통과 (0.61ms, 10.4MB)
테스트 29 〉 통과 (0.74ms, 10.3MB)
테스트 30 〉 통과 (0.61ms, 10.4MB)
테스트 31 〉 통과 (1.20ms, 10.1MB)
테스트 32 〉 통과 (0.63ms, 10.1MB)
테스트 33 〉 통과 (0.00ms, 10.3MB)
효율성 테스트
테스트 1 〉 통과 (68.22ms, 16.7MB)
테스트 2 〉 통과 (69.11ms, 16.7MB)
테스트 3 〉 통과 (68.94ms, 16.7MB)
테스트 4 〉 통과 (63.09ms, 17.5MB)- 대부분 비슷하다.
- 이쪽이 가독성이 더 좋다.
def solution(sticker):
n = len(sticker)
if n <= 3:
return max(sticker)
dp1 = [0] * n
dp2 = [0] * n
dp1[0] = sticker[0]; dp1[1] = dp1[0]
dp2[1] = sticker[1]; dp2[0] = 0
# case 1 -> pick 0
for i in range(2, n-1):
dp1[i] = max(dp1[i - 2] + sticker[i], dp1[i - 1])
for i in range(2, n):
dp2[i] = max(dp2[i - 2] + sticker[i], dp2[i - 1])
return max(dp1[-2], dp2[-1])
정확성 테스트
테스트 1 〉 통과 (0.00ms, 10.3MB)
테스트 2 〉 통과 (0.00ms, 10.2MB)
테스트 3 〉 통과 (0.01ms, 10.2MB)
테스트 4 〉 통과 (0.01ms, 10.2MB)
테스트 5 〉 통과 (0.01ms, 10.2MB)
테스트 6 〉 통과 (0.02ms, 10.1MB)
테스트 7 〉 통과 (0.70ms, 10.2MB)
테스트 8 〉 통과 (0.53ms, 10.2MB)
테스트 9 〉 통과 (1.10ms, 10.2MB)
테스트 10 〉 통과 (0.53ms, 10.1MB)
테스트 11 〉 통과 (0.53ms, 10.3MB)
테스트 12 〉 통과 (0.52ms, 10.1MB)
테스트 13 〉 통과 (0.52ms, 10.1MB)
테스트 14 〉 통과 (0.54ms, 10.2MB)
테스트 15 〉 통과 (0.55ms, 10.3MB)
테스트 16 〉 통과 (0.54ms, 10.4MB)
테스트 17 〉 통과 (0.51ms, 10.1MB)
테스트 18 〉 통과 (0.59ms, 10.2MB)
테스트 19 〉 통과 (0.52ms, 10.2MB)
테스트 20 〉 통과 (0.56ms, 10.4MB)
테스트 21 〉 통과 (0.56ms, 10.2MB)
테스트 22 〉 통과 (0.55ms, 10MB)
테스트 23 〉 통과 (0.54ms, 10.2MB)
테스트 24 〉 통과 (0.52ms, 10.1MB)
테스트 25 〉 통과 (0.65ms, 10.2MB)
테스트 26 〉 통과 (0.63ms, 10.3MB)
테스트 27 〉 통과 (1.05ms, 10.3MB)
테스트 28 〉 통과 (1.01ms, 10.4MB)
테스트 29 〉 통과 (0.54ms, 10.2MB)
테스트 30 〉 통과 (0.54ms, 10.1MB)
테스트 31 〉 통과 (0.52ms, 10.2MB)
테스트 32 〉 통과 (0.55ms, 10.1MB)
테스트 33 〉 통과 (0.00ms, 10.2MB)
효율성 테스트
테스트 1 〉 통과 (58.76ms, 16.7MB)
테스트 2 〉 통과 (58.67ms, 16.7MB)
테스트 3 〉 통과 (59.07ms, 16.7MB)
테스트 4 〉 통과 (58.46ms, 17.6MB)- DP를 좀 더 공부해야할 듯.
- 근데 DP가 결국은 점화식을 만들어내는 거라서
- 그게 생각처럼 잘 되질 않는다.
728x90
반응형
'게임 프로그래밍 > Python 프로그래밍' 카테고리의 다른 글
| 프로그래머스 덧칠하기 (for문) (0) | 2023.03.02 |
|---|---|
| 프로그래머스 바탕화면 정리 (for문, 행열 훼이크) (6) | 2023.03.02 |
| 프로그래머스 입국심사 (이분탐색) (0) | 2023.03.01 |
| 프로그래머스 수식 최대화 (2020 카카오 인턴쉽, 순열, 정규표현식, 연산자) (0) | 2023.03.01 |
| 프로그래머스 [3차] 방금그곡 (2018 KAKAO BLIND RECRUITMENT, 문자열 변환 (0) | 2023.02.28 |